Trapezio
Un trapezio è un quadrilatero con due soli lati paralleli.
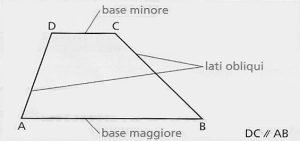
- I due lati paralleli si chiamano basi, una è la base maggiore, l'altra la base minore.
- I due lati obliqui, non paralleli, vengono chiamati semplicemente lati del trapezio.
- La distanza fra le due basi è l'altezza del trapezio.
Formule per un trapezio qualsiasi
| Perimetro: | \(P = b+ B + l_1 + l_2\) |
| Area: | \(A = \frac{(B + b)h}{2}\) |
| Base maggiore: | \(B = \left( \frac{2A}{h} \right) - b\) |
| Base minore: | \(b = \left( \frac{2A}{h} \right) - B\) |
| Altezza: | \(h = \frac{2A}{b + B}\) |
Trapezio isoscele
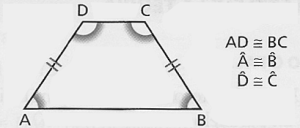
Un trapezio isoscele è un trapezio avente i lati obliqui congruenti.
- Un trapezio isoscele ha gli angoli adiacenti a ciascuna base congruenti.
- E' sufficiente che gli angoli adiacenti a ciascuna base siano congruenti affinché un trapezio sia isoscele.
Per il trapezio isoscele valgono le seguenti congruenze:
- \(AD \cong BC\) (lati obliqui congruenti)
- \(\hat A \cong \hat B\) (angoli adiacenti alla base maggiore congruenti)
- \(\hat D \cong \hat C \) (angoli adiacenti alla base minore congruenti)
Formule aggiuntive per un trapezio isoscele
| Perimetro: | \(P = B + b + 2L\) |
| Lato: | \(L = \sqrt{h^2+\left[\frac{(B - b)}{2}\right]^2}\) |
| Altezza: | \(h = \sqrt{L^2+\left[\frac{(B - b)}{2}\right]^2}\) |
Trapezio rettangolo
Un trapezio rettangolo è un trapezio avente uno dei lati perpendicolare alle basi.
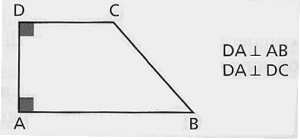
Formule aggiuntive per un trapezio rettangolo
| Lato obliquo: | \(L = \sqrt{h^2 + (B - b)^2}\) |
| Altezza con D e B: | \(h = \sqrt{D^2 - B^2}\) |
| Altezza con d e b: | \(h = \sqrt{d^2 - b^2}\) |
| Diagonale maggiore: | \(D = \sqrt{B^2 + h^2}\) |
| Diagonale minore: | \(d = \sqrt{b^2 + h^2}\) |
| Base maggiore: | \(B = \sqrt{D^2 - h^2}\) |
| Base minore: | \(b = \sqrt{d^2 - h^2}\) |